二进制数的科学计数法

C++中使用的浮点数包括采用的是IEEE标准下的浮点数表示方法。我们知道在数学中可以将任何十进制的数写成以10为底的科学计数法的形式，如下

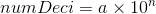
其中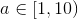显而易见，因为如果a比10大或者比1小都能够再次写成10的指数的形式，如

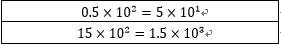
然而要想在二进制的世界中将数字写成以10为底的科学计数法的形式，着实有点麻烦，因为你首先需要将二进制的数先化成10进制的表示方法，然后才能写成科学计数法的形式。但是如果我们稍微变通一下科学计数法的标记方法，问题就变得特别的简单了。之所以数学上使用的科学计数法选用10为底，是因为我们通常使用的计数方式是十进制的。在计算机的世界中我们使用的数却是二进制的，所以我们在这个世界中应该改用以2为底的科学计数法而不是10为底的科学计数法。此时我们使用的科学计数法就表示成了如下形式，

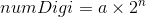
对于一个二进制的数来说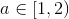是不言而喻的，以为例

IEEE 754标准下的存储策略

IEEE标准下的浮点数存储包括三个基本的组成：符号位、指数、尾数（the sign, the exponent, the mantissa），尾数是由小数部分和一个隐含的前导数位组成。至于前导数位隐含的原因很简单（下面将会解释）。

下面的表格展示了计算机存储单精度和双精度浮点数的层次结构，包括每一部分的比特位（比特范围用方括号括出，00表示最低位）

Floating Point Components

	Sign	Exponent	Fraction
Single Precision	1 [31]	8 [30-23]	23 [22-00]
Double Precision	1 [63]	11 [62-52]	52 [51-00]

• 符号位

符号位非常简单，位于存储浮点数的最高比特位，且只占1比特。0表示正数，1表示负数。通过改变该比特位的值可以改变该浮点数的符号。

• 指数位

因为指数位既需要能够表示正指数也需要能够表示负指数，为了能够做到这一点，需要将真实的指数数值加上一个偏移值获得用来存储的指数值。对于IEEE标准下的单精度浮点数，这个偏移值是127。因此当真实的指数为0的时候，我们存储的指数位为127。如果存储的指数值是200，那么真实的指数值就应该是（200-127），即73。后面的原因会指出，指数为-127（指数位全为0）和+128（指数位全为1）会被用来存储特殊的数值。

对于双精度的浮点数，指数位的长度位11比特，偏移量位1023。

• 尾数

尾数也被称为有效数位（significand）,决定浮点数的精确度。它由隐含的前导数位（小数点左边的部分）和小数部分（小数点右边的部分）组成，因为我们采用以2为底的科学计数法表示二进制数，那么小数点左边的尾数部分自然是固定值1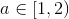（），所以前导数位我们不需要明确的表示出来，我们只需要存储尾数的小数部分就可以了。

浮点数存储示例

下面就以单精度浮点数来浮点数的存储策略。

十进制数0.15625₁₀ 写成二进制的形式为0.00101_2。通过乘以以2为底的指数，将小数点向右移动3位后得到

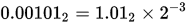
这个时候我们就能够确定它的尾数的小数部分和指数分别是多少了，尾数的小数部分位.01_2，指数为-3。具体存储方法见下图，

在IEEE 745标准下，我们用三部分来表示一个浮点数：

• sign = 0, 因为该浮点数为正数（用1表示负数）;
• 真实的指数是-3，但是我们用来存储的指数要在真实的指数上加上偏移量。在单精度浮点数中，这个偏移量是127，在双精度浮点数中这个偏移量是1023；所以我们这里用来存储的指数应该为（-3+127），即124。

浮点数的范围

我们先来考虑单精度浮点数的范围问题。注意到我们用来存储双精度浮点数的是一块长为32bits的内存，我们重新解释了一下该快内存中数字的存储规则使得表示数的范围大大增加。但是我们看看这样子带来了什么问题？

对于32bits的无符号整数来说，它可以表示0~2³²-1范围内的任意整数。但是单精度的浮点数却做不到这一点，因为浮点数的存储策略中用来存储尾数的长度只有24bits，这个时候单精度浮点数就会把将底位的部分截断，例如

11110000 11001100 10101010 10101111  // 32-bit integer= +1.1110000 11001100 10101011 x 2^31     // Single-Precision Float=   11110000 11001100 10101011 00000000  // Corresponding Value

 这样的方法可以近似32bits的值，但是并不能得到准确的结果。忽略精确度的问题，浮点数能够表示的范围是2¹²⁷，而32bits整数的表示范围是2³²。

特殊值

• 零

按照上面的浮点数表示方法，我们发现并不能表示出数值0的大小。因为我们认为前导数位的值永远为0，这个时候无论尾数的小数部分和指数部分怎么取，浮点数的值都不会是0。为此我们规定，当指数位全部为0且尾数的小数位全为0时，这个时候浮点数的值为0。注意，+0和-0时两个不同的浮点数，即使他们的数值一样，但是浮点数的表示方式不一样。

• 非标准化的值

当指数部分全为0，但时小数位不全为0的时候，这个时候浮点数表示的值就是非标准化的值。这个时候我们认为该浮点数的前导数位为0，因此这个时候的单精度浮点数大小为(−1)^s × 0.f × 2⁻¹²⁶，双精度浮点数的大小为(−1)^s × 0.f × 2⁻¹⁰²²，其中s为符号位上的数值，2为底的指数分别是-126和-1022，而不是-127和-1023。具体原因很简单，因为标准化所能表示的最小值是(−1)^s × 1 × 2⁻¹²⁶和(−1)^s × 1× 2⁻¹⁰²²。提出非标准化的目的就是为了表示更小的值从而提高精确度。

• 无穷大

当指数位全为1，而尾数的小数部分全为0时表示+∞和−∞，同时通过符号位来区分+∞和−∞。所以采用IEEE 754标准表示浮点数可以很好的处理无穷大的情况。

• 非数字(NaN)

NaN(Not a Number)用来表示非数字的值，当指数位全为1且尾数的小数部分不为0时表示NaN值。一共有两类NaN值，静态非数（QNaN, Quiet NaN）和警告非数(SNaN, Signalling NaN)。

在一个NaN的值中，如果尾数小数部分首位被置位则表示QNaN。QNaN是很重要的一类非数，四则运算经常传递QNaN值，该值通常表示不被数学上定义的运算结果，比如除数为零的时候。

在一个NaN的值中，如果尾数小数部分首位被置0则表示SNaN。它别用来表示操作中的一个异常，可以用来表示一个未被初始化变量的过早使用。

 

 Reference：

[1] http://steve.hollasch.net/cgindex/coding/ieeefloat.html

[2] https://en.wikipedia.org/wiki/IEEE_754-1985